로지스틱 회귀분석은 독립변수의 선형 결합을 이용 발생 가능성을 예측하는데 사용되는 통계 기법입니다.
로지스틱 회귀분석은 선형회귀 분석과 비슷해 보이지만 종속변수로 범주형 데이터를 사용한다는 특징이 있습니다.
이를 이용하여 코딩하고 결과를 예측해보도록하겠습니다.
getwd()
setwd('/Users/sik/Desktop/dataset4')
install.packages('ROCR')
library(ROCR)사용되는 패키지는 다음과 같습니다.
로지스틱 회귀함수로 glm() 은 내장 패키지이므로 따로 설치할 필요가 없습니다.
ROCR은 로지스틱 회귀를 한뒤 모델을 평가하기위해서 사용되는 패키지로 ROC커브평가를 할수있습니다.
weather = read.csv('weather.csv', stringsAsFactors = F)
dim(weather)
head(weather)
str(weather)이번에는 날씨데이터를 이용하여 다음날 비가 올지 오지 않을지에 대한 분류를 해보겠습니다
데이터의 구조는 다음과 같습니다.
'data.frame': 366 obs. of 15 variables:
$ Date : chr "2014-11-01" "2014-11-02" "2014-11-03" "2014-11-04" ...
$ MinTemp : num 8 14 13.7 13.3 7.6 6.2 6.1 8.3 8.8 8.4 ...
$ MaxTemp : num 24.3 26.9 23.4 15.5 16.1 16.9 18.2 17 19.5 22.8 ...
$ Rainfall : num 0 3.6 3.6 39.8 2.8 0 0.2 0 0 16.2 ...
$ Sunshine : num 6.3 9.7 3.3 9.1 10.6 8.2 8.4 4.6 4.1 7.7 ...
$ WindGustDir : chr "NW" "ENE" "NW" "NW" ...
$ WindGustSpeed: int 30 39 85 54 50 44 43 41 48 31 ...
$ WindDir : chr "NW" "W" "NNE" "W" ...
$ WindSpeed : int 20 17 6 24 28 24 26 24 17 6 ...
$ Humidity : int 29 36 69 56 49 57 47 57 48 32 ...
$ Pressure : num 1015 1008 1007 1007 1018 ...
$ Cloud : int 7 3 7 7 7 5 6 7 7 1 ...
$ Temp : num 23.6 25.7 20.2 14.1 15.4 14.8 17.3 15.5 18.9 21.7 ...
$ RainToday : chr "No" "Yes" "Yes" "Yes" ...
$ RainTomorrow : chr "Yes" "Yes" "Yes" "Yes" ...
다소 불필요하다 생각되는 컬럼이 존재해 보입니다.
weather_df <- weather[, c(-1, -6, -8, -14)]
weather_df
str(weather_df)
weather_df$RainTomorrow이렇게 인덱싱을 통하여 편하게 컬럼을 제거 할 수 있습니다.
이번에는 범주화를 시켜보도록 하겠습니다. 로지스틱 회귀분석의 경우는 종속변수의 범주화가 필요합니다. 따라서 0과 1로 범주화를 해주는 코딩을 해보겠습니다.
weather_df$RainTomorrow[weather_df$RainTomorrow == 'Yes'] <- 1
weather_df$RainTomorrow[weather_df$RainTomorrow == 'No'] <- 0
weather_df$RainTomorrow <- as.numeric(weather_df$RainTomorrow)
head(weather_df$RainTomorrow)이렇게 입력해주면 'Yes'값은 1 'No'값은 0으로 변환 해줄수 있습니다.
> head(weather_df$RainTomorrow)
[1] 1 1 1 1 0 0문자형이었던 변수들이 모두 정수형으로 변환된 것을 볼 수 있습니다.
이제 예측을 하기위해서 가지고있는 데이터셋을 훈련용데이터와, 테스트 데이터로 나누어 보도록하겠습니다.
idx <- sample(1:nrow(weather_df), nrow(weather_df)*0.7)
train <- weather_df[idx, ]
test <- weather_df[-idx, ]
train
test
train = na.omit(train)
test = na.omit(train)
nrow(test)
test[1:110, ]
tail(test, 30)위의 분할은 트레이닝 70%, 테스트 30%의 데이터 셋을 분할한 값을 같습니다.
원래 데이터 셋에 NA값이 들어 있으므로 제거해주도록하겠습니다.
결측값은 함부로 제거하면 안되지만 이번의경우 다수의 컬럼에 조금씩 들어있어 결측값을 제거하겠습니다.
weather_model <- glm(RainTomorrow ~ ., data = train, family = 'binomial', na.action = na.omit)
weather_model # train 셋에 NA값이 위치 할 경우
summary(weather_model)로지스틱 회귀모형으로 학습을 시킨뒤 결과값을 보도록 하겠습니다.
Deviance Residuals:
Min 1Q Median 3Q Max
-2.43783 -0.37098 -0.16582 -0.06205 2.48916
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 100.26363 45.62468 2.198 0.02798 *
MinTemp -0.22823 0.08908 -2.562 0.01040 *
MaxTemp 0.30308 0.23338 1.299 0.19408
Rainfall -0.10006 0.07271 -1.376 0.16878
Sunshine -0.32101 0.13202 -2.432 0.01504 *
WindGustSpeed 0.08023 0.02791 2.874 0.00405 **
WindSpeed -0.07058 0.04051 -1.742 0.08143 .
Humidity 0.09463 0.03368 2.810 0.00496 **
Pressure -0.11133 0.04422 -2.518 0.01182 *
Cloud 0.19417 0.14092 1.378 0.16826
Temp 0.06286 0.24928 0.252 0.80092
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 239.91 on 252 degrees of freedom
Residual deviance: 124.13 on 242 degrees of freedom
AIC: 146.13다음과 같은 결과값을 갖습니다. 많은 변수중에 유의미한 변수는 5개정도로 볼 수 있겠습니다.
이제 분류정확도를 확인해보겠습니다.
다음과 같은 코드를입력해보겠습니다.
table(result_pred, test$RainTomorrow)교차테이블로 확인한결과 상당히 잘 분류한 것을 볼 수있습니다.
result_pred 0 1
0 200 16
1 7 30분류 정확도를 확인해 보겠습니다.
> acc = (200+30) / (200 + 16 + 7 + 30)
> acc
[1] 0.909090990퍼센트의 높은 분류율을 보여주는 것을 볼 수 있습니다.
데이터의 양이 아주 작기때문에 이 분류율을 맹신해서는 안됩니다.
이제 ROC커브로 모델의 평가를 해보도록 하겠습니다.
pr <- prediction(pred, test$RainTomorrow)
prf <- performance(pr, measure = 'tpr', x.measure = 'fpr')
plot(prf)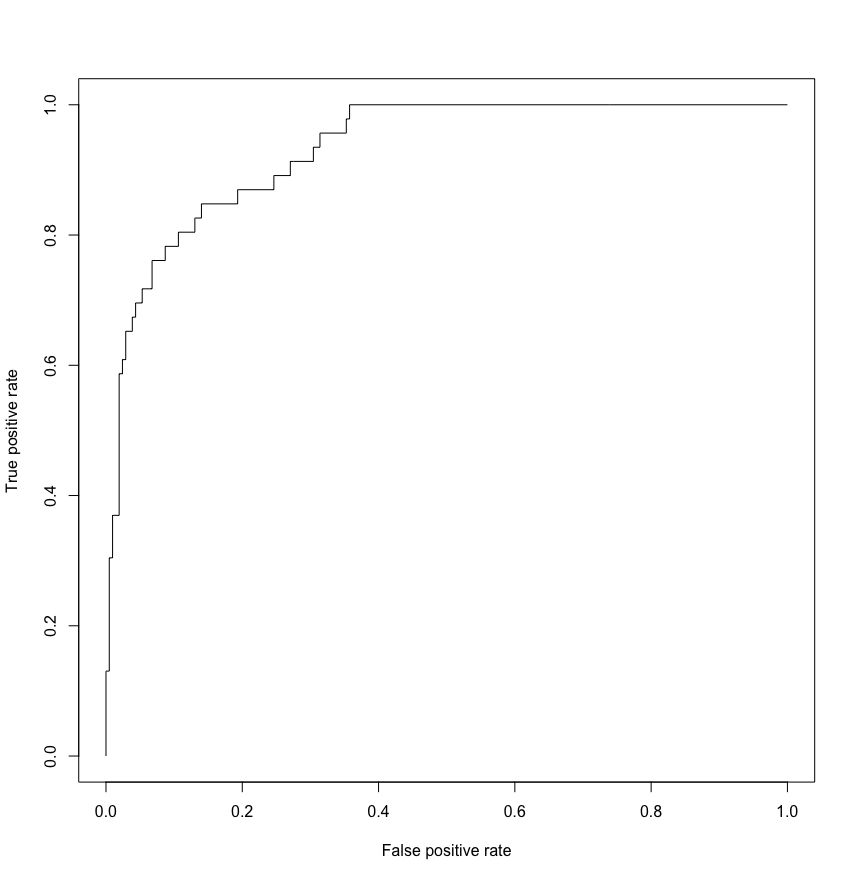
ROC커브는 직각을 이루면 가장 완벽한 그래프가 되지만 그러기에는 쉽지않겠습니다.
위 그래프를보면 상당히 좋은 결과를 나타냄을 알 수 있습니다.
'R > Machine-Learning' 카테고리의 다른 글
| R을 이용한 머신러닝 알고리즘 -부스팅- (0) | 2022.03.12 |
|---|---|
| R을 이용한 머신러닝 알고리즘 -배깅- (0) | 2022.03.12 |
| R을 이용한 머신러닝 알고리즘 -랜덤포레스트- (0) | 2022.03.12 |
| R을 이용한 머신러닝 알고리즘 -군집분석 2- (0) | 2022.03.07 |
| R을 이용한 머신러닝 알고리즘 -군집분석 1- (0) | 2022.03.07 |


